一种全新的化合物分子表示方法:SELFIES (Self-Referencing Embedded Strings) 解读
作者:くろたんく
译者:石峪成
前言
本文旨在介绍一种名为 SELFIES 的新型分子表示方法,该方法由因开发 Chemical VAE 而闻名的 Aspuru-Guzik 教授团队研发并首次在论文中提出,于 2019 年发布在 arXiv 上。
原文标题:Self-referencing embedded strings (SELFIES): A 100% robust molecular string representation
作者:Mario Krenn、Florian Häse、AkshatKumar Nigam、Pascal Friederich、Alan Aspuru-Guzik
发表期刊:Machine Learning: Science and Technology
发布日期:2020 年 10 月 28 日
DOI:10.1088/2632-2153/aba947
本文不仅基于论文内容,还结合实际运行代码和实现细节进行了解释,力求简洁明了、便于读者理解。如果您对此感兴趣,建议参考相关论文和代码实现以获取更深入的信息。
此外,本文的内容基于 SELFIES 的 v1.0.4版本。(译者注:目前已更新至v2.1.2)
Github repository: https://github.com/aspuru-guzik-group/selfies/tree/master
请注意,由于在论文发表后 SELFIES 的开发工作取得了显著进展,论文中的描述与 v1.0.4 版本的输出可能存在一定差异。因此,您在阅读本文时可能会发现部分内容与论文不完全一致而感到疑惑(实际上,我也曾因这个问题而感到困惑……)。
背景
由于找不到任何关于 SELFIES 的详尽的语法解读,而我又希望将其应用于自己的研究,因此想加深对这种新的表示方法的理解。正当我考虑自己撰写解读时,论文的第一作者 Mario Krenn 主动联系了我,并表示支持我撰写关于 SELFIES 的博客。因此,我重新仔细阅读了论文,并对论文描述与当前版本的 SELFIES 行为差异进行了研究,几乎完全掌握了其语法。基于此,我决定撰写这篇解读文章。
论文概述
目前,SMILES 是一种被广泛用于表示化合物分子的标准格式。然而,当用 SMILES 作为生成模型的输入或输出时,常常会出现相当大比例的无效分子。这主要是由于生成的字符串在语法上无效,或违反了化学的基本规则,例如原子间的最大化学键数等。为了解决上述问题,研究者们开发了 SELFIES。
SELFIES 的一大特点是,即使是完全随机生成的 SELFIES 字符串,也能正确地表示一个合法的分子图。为了实现这一点,作者们借助了理论计算机科学中的概念,例如形式语法(formal grammar)和形式自动机(formal automatons),具体而言是 Chomsky 第二型文法(形式上下文无关文法)或有限状态自动机的思想来设计 SELFIES。
在论文中,作者使用 SELFIES 和 SMILES 对分子生成模型(如 VAE 和 GAN)进行了实验。结果表明,与使用 SMILES 相比,使用 SELFIES 时输出分子完全有效,并且模型能够生成多样性远超预期的分子集合。这进一步证明了 SELFIES 的优越性。(论文中的Table 1, Figure 5, Figure 6)
(个人认为)SELFIES 的卓越之处
环和分支的编码方式独特
与通过字符串明确标记环(Ring)和分支(Branch)的起点和终点的传统方法不同,SELFIES 通过直接用长度表示环和分支。这种方式通过环或分支符号之后的数字表示长度,从而有效规避了语法问题(这一点将在后文中提到与索引符号相关的细节)。
考虑化合价的符号化设计
SELFIES 在编码过程中充分考虑了化合价的约束。例如,C=C=C(三个碳通过双键连接)是被允许的,而 F=O=F(氟与氧形成双键)则是不可能的,因为氟最多只能形成一个键,而氧最多只能形成两个键。SELFIES 的设计确保生成的分子始终满足这些化合价约束。
生成结果的有效性
我个人尝试使用图神经网络(GNNs)对分子进行编码,测试了基于 VAE 的分子到 SELFIES(Mol to SELFIES)和分子到 SMILES(Mol to SMILES)的生成模型。结果发现,无论是 SMILES 还是 SELFIES,生成过程本身都能正常进行。但在生成有效分子时,使用 SMILES 时只有少数是有效的,而使用 SELFIES 时有效率达到 100%。
(具体实验结果将在其他场合详细分享。)
基于SELFIES表示的其他研究成果
根据上述论文的实验结果,SELFIES 在基于深度生成模型或遗传算法的功能性分子逆向设计任务中展现出了卓越的表现。事实上,已有越来越多的研究开始采用 SELFIES,并取得了显著的成果。
基于遗传算法的逆向设计
分子图到SMILES的转换
SMILES到IUPAC名称的转换
SELFIES的语法解读(正文)
关于SMILES
在深入讨论 SELFIES 之前,读者有必要对 SMILES 具有基本的了解。如果您对 SMILES 的概念还不熟悉,那么本文的内容可能会显得难以理解。本文默认读者对 SMILES 有一定程度的认识。
如果您对 "SMILES 是什么" 这一问题尚有疑惑,建议首先阅读 py4chemoinformatics(https://github.com/Mishima-syk/py4chemoinformatics),以掌握 SMILES 的基础知识,同时学习 RDKit 的使用方法,积累相关领域的知识。这样将更有助于理解 SELFIES 的核心内容。
此外,阅读金子教授的著作(https://www.amazon.co.jp/exec/obidos/ASIN/4274224414/blacktanktoph-22/)也是一个不错的选择。这本书系统介绍了化学数据的解析方法以及如何将这些数据应用于机器学习的相关知识。通过阅读本书,您可以全面掌握从数据处理到模型应用的整个流程,为进一步理解 SELFIES 和相关技术奠定扎实的基础。
包含 SMILES 在内的其他分子表示方法
关于 SMILES 及其他分子表示方法的简要说明,建议参考 @steroidinlondon 的相关内容(https://aimedchem.hatenablog.com/entry/2020/09/30/071203)。他对这些表示方法进行了清晰的解释,阅读后能够帮助您快速了解相关概念。
MDMA 解读(一次初步的观察)
接下来,我们正式开始解读。
首先,在论文的 Figure 1 中出现了 MDMA(3,4-Methylenedioxymethamphetamine)的 SMILES 表示,通过 Colab 和 RDKit 使用 Chem.MolFromSmiles("CNC(C)CC1=CC=C2C(=C1)OCO2") 处理后,可以将其分子结构绘制出来,结果如下图所示。

也就是说,MDMA 的 SMILES 表示是 CNC(C)CC1=CC=C2C(=C1)OCO2。
那么,MDMA 的 SELFIES 表示是什么呢?
使用以下代码:
- import selfies as sf
- sf.encoder("CNC(C)CC1=CC=C2C(=C1)OCO2")
- # [C][N][C][Branch1_1][C][C][C][C][=C][C][=C][C][Branch1_2][Ring2][=C][Ring1][Branch1_2][O][C][O][Ring1][Branch1_2]
从直观感受上来看,SELFIES 表示中的 "C" 数量似乎比原始 SMILES 中更多。直接从 MDMA 开始理解 SELFIES 的语法可能过于复杂,因此我们从更简单的例子入手。
为了掌握 SELFIES 的语法,需要理解以下四个核心符号体系:原子符号(Atomic Symbols)、索引符号(Index Symbols)、分支符号(Branch Symbols) 和 环符号(Ring Symbols)。只要对这些概念有了清晰的认识,就可以基本理解SELFIES了。
原子符号(Atomic Symbols)
首先,我们来看看一个简单的示例。
- sf.encoder("C=CC#C[13C]")
- # [C][=C][C][#C][13Cexpl]
- sf.encoder("CF")
- # [C][F]
- sf.encoder("COC=O")
- # [C][O][C][=O]
原子符号由 键类型(bond type)和 原子类型(atom type)组成,并用方括号 [] 括起来表示。
- 键类型(bond type)的表示方法与 SMILES 相同:
- 单键:' '(空,即无符号)
- 双键:'='
- 叁键:'#'
- 几何异构体:'/' 和 '\\'
- 原子类型(atom type) 的表示方法也与 SMILES 相同。然而,当显式使用方括号(如 [13C] 或 [C@@H])时,SELFIES 会在原子符号后附加一个 expl 字符。此外,SELFIES 同样支持离子的表示。
SELFIES 的高有效性归因于其解码器(Decoder)的设计。下面用一个示例来说明这一点。
- # 与上面的例子相同,再次展示
- sf.encoder("COC=O")
- # [C][O][C][=O]
- sf.decoder("[C][O][C][=O]")
- # COC=O
- # 即使随意书写不符合价数规则的化合物,也只能解码到可能的部分
- sf.decoder("[C][O][=C][#O][C][F]")
- # COC=O
正如上述例子所示,当某些键的连接方式违反了前一个原子或当前原子的键合约束时,SELFIES 会自动调整,以确保所有键合约束得到满足。这是通过(尽可能少地)降低键的多重性(译者注:如上述例子中把C和O形成的叁键降为双键)来实现的。(关于价数的相关描述可以参考代码中的 XXXXX_bond_constraints 部分。)
到目前为止,您应该已经可以理解简单的直链分子表示方法了。接下来,我将解释分支符号(Branch Symbols)和环符号(Ring Symbols)。不过,在前面提到的 MDMA 示例中,我们发现 SELFIES 表示中的 "C" 似乎比原始 SMILES 更多,这一问题还需解决。要理解这一点,必须先介绍与分支符号和环符号密切相关的 索引符号(Index Symbols)。
索引符号(Index Symbols)
这是我个人感到非常困惑的部分之一,正如前文所述:
“与通过字符串明确标记环(Ring)和分支(Branch)的起点和终点的传统方法不同,SELFIES 通过直接用长度表示环和分支。这种方式通过环或分支符号之后的数字表示长度,从而有效规避了语法问题。”
这是什么意思呢?也就是说,表示原子、分支结构和环状结构的字符串会被视为一种索引(index)。
关于这一点,可以参考相关描述:
用表格表示如下:
| idx()值 | 符号 |
| 0 | [C] |
| 1 | [Ring1] |
| 2 | [Ring2] |
| 3 | [Branch1_1] |
| 4 | [Branch1_2] |
| 5 | [Branch1_3] |
| 6 | [Branch2_1] |
| 7 | [Branch2_2] |
| 8 | [Branch2_3] |
| 9 | [O] |
| 10 | [N] |
| 11 | [=N] |
| 12 | [=C] |
| 13 | [#C] |
| 14 | [S] |
| 15 | [P] |
论文中频繁出现的术语 𝑄,指的正是这一概念。按照十六进制的规则,可以通过以下公式表示 𝑄:
为便于理解,我们通过分支符号(Branch Symbols)的例子来更快地了解这个公式的含义。
分支符号(Branch Symbols)
由上述公式可以知道,通过索引符号可以计算出 𝑄 的值。接下来,我们来看一个包含分支结构的例子。
- # SO4
- sf.encoder("S(=O)(=O)([O-])[O-]")
- # [S][Branch1_2][C][=O][Branch1_2][C][=O][Branch1_1][C][O-expl][O-expl]

首先,分支符号(Branch Symbols)遵循 [Branch{L}_{M}] 的模式。左侧的 L 取值范围为 {1, 2, 3},表示需要查看后续字符中多少个符号作为索引符号(Index Symbols)。如果是 1,则查看 1 个字符;如果是 2,则查看 2 个字符。在这个示例中,没有查看到 2 个字符的情况。需要查看 2 个字符的情况通常假定为长链,例如连续 17 个或更多的 "C"(稍后会介绍)。
接着,[Branch{L}_{M}] 的右侧 M 的取值范围也为 {1, 2, 3},表示与索引符号后的原子间的键合模式。单键用 1 表示,双键用 2 表示,叁键用 3 表示。显然,这种关系与对应的原子符号(Atom Symbol)是相关联的。需要注意的是,如果某一项未满足(例如前一个原子或当前原子的键合约束被违反),正如前面所说,“当某些键的连接方式违反了前一个原子或当前原子的键合约束时,SELFIES 会自动调整,以确保所有键合约束得到满足。这是通过(尽可能少地)降低键的多重性来实现的。”
以 SO₄ 的 [Branch1_2] 为例:
后续索引符号仅查看 1 个字符,因此 [C] 是唯一被处理为索引符号的部分。在先前的表中,[C] 的索引为 0。这里需要特别注意的是,分支结构的范围是通过从索引符号计算得出的 𝑄 值决定的。分支结构的范围包括 𝑄+1 个符号。在本例中,由于所有的分支符号后的索引符号都是 [C],因此分支结构仅包含 0+1=1 个符号(即 [=O] 或 [O-expl])。
如果将没有分支符号(Branch Symbols)的部分视为直接连接的结构,会更容易理解(在本例中,分子头部和尾部的[S]和[O-expl]分别直接相连,而其他三个部分被视为分支结构)。
此外,类似 [Branch2_1] 的情况,例如以下例子中可能出现的长链,虽然极为罕见,但从原理上是可以实现的。由于分支符号的设计支持 3 级分支,因此理论上最多可以表示长达 16³ 个碳原子的超长链。
(译者注:这里可能有些难懂,这些索引符号本身并不表示任何含义,它们只用于表示数值。根据上文中提到的𝑄值计算公式,团队在这里用了一种巧妙的方法将三个索引表中的符号直接映射成一个三位的十六进制数,这样就可以用于表示0-4095的任意一个值,并且保证每个符号组合都有一个唯一的𝑄值。)

环符号(Ring Symbols)
到这里为止,如果您已经理解了分支符号(Branch Symbols),那么环符号(Ring Symbols)就非常简单了。
环符号主要有两种模式:[Ring{L}] 和 [ExplRing{L}]。其中 L 的取值范围是 {1, 2, 3},表示需要查看后续多少个字符作为索引符号(Index Symbols)。与分支符号类似,通过计算 𝑄 的值,将当前符号与 𝑄+1 个位置之前的原子符号(Atomic Symbols)连接,形成环状结构。
下面通过一个例子来说明这一点。大家最喜欢(也许?)的苯环是一个很好的示例,非常直观易懂。
- sf.encoder("C1=CC=CC=C1")
- # [C] [=C] [C] [=C] [C] [=C] [Ring1] [Branch1_2]
- # ↑ ↑ ↑ ↑ ↑ ↑
- # 5 4 3 2 1 基准
需要注意的是,在 [Ring1] 之后的内容是索引符号(Index Symbols)。这里出现了 [Branch1_2],但在这种情况下,它仅被视为一个索引符号。由于是 [Ring1],所以作为索引符号的只有后续的一个字符,即 [Branch1_2]。在索引符号表中,[Branch1_2] 的索引值为 𝑄 = 4,因此 𝑄+1 个位置之前的 原子符号是前面的第 5 个符号,也就是SELFIES中最开始的 [C]。通过与这个 [C] 的结合,形成了环状结构。
至于 [ExplRing{L}] 模式,可以通过苯环的另一种表示方式来理解。苯环用 SMILES 也可以表示为 C=1C=CC=CC=1。将其转为 SELFIES 时,表示如下:
- sf.encoder("C=1C=CC=CC=1")
- # [C] [C] [=C] [C] [=C] [C] [Expl=Ring1] [Branch1_2]
- # ↑ ↑ ↑ ↑ ↑ ↑
- # 5 4 3 2 1 基准
上述示例和前面示例的基本原理是相同的,但由于这里写作 [Expl=Ring1],表示在与环状结构形成连接时,基于环符号(Ring Symbols)指代的原子符号(Atomic Symbols)(译者注:这里指5号碳原子),需要将键类型(bond type)设置为 "="。可以将其理解为 SMILES 中最后的 =1 相对应的一种表示方式。
补充说明
环符号(Ring Symbols)还有一些有趣的特性,例如可以用环符号表示类似乙炔(Acetylene)这样的叁键。其原理看起来是:在已经用单键连接的部分,通过添加双键形成环状结构,从而实现叁键的构造。
- sf.decoder("[C][C][Expl=Ring1][C]")
- # C#C
MDMA 解读
到这里为止,您应该已经能够完全理解之前展示的 MDMA 的 SELFIES 表示了。
- import selfies as sf
- sf.encoder("CNC(C)CC1=CC=C2C(=C1)OCO2")
- # [C][N][C][Branch1_1][C][C][C][C][=C][C][=C][C][Branch1_2][Ring2][=C][Ring1][Branch1_2][O][C][O][Ring1][Branch1_2]

虽然没有很好地实现颜色区分,可能显得稍微有些难以理解,但如果综合利用之前介绍的所有基础知识,应该能够毫无问题地理解。
较为复杂的部分在中间的 [Branch1_2][Ring2][=C][Ring1][Branch1_2],这里是通过将分支结构的末端连接到环状结构形成的。这部分的逻辑相对复杂,但只要稍加认真思考,应该可以理解其机制。
Colab
为了能够方便地反复试验,我在Google Colab上进行了所有操作。代码已经开放,您可以自行查看。如果有需要,您也可以根据自己的需求修改、下载并尝试运行,进行各种探索和实验。
总结
通过以上内容,相信您已经对 SELFIES 的语法有了近乎完全的理解。
那么,为什么与 SMILES 不同,以 SELFIES 形式描述的分子能更有效地应用于 VAE、GAN 等生成模型呢?虽然我可能还有一些细节尚未完全理解,但根据我的看法,其核心优势在于:SELFIES 即使随机排列,也能 100% 表示有效的化合物,这种超高的鲁棒性(robustness)意味着潜在空间中不存在无效区域。这一点对于生成模型的有效性至关重要。
我也在思考,是否能将 SELFIES 高效地应用于我的研究中。
结语
尝试将自己理解的复杂内容用简单易懂的方式讲解,一直以来都让我感到是件不容易的事。
这篇文章最终竟然超过了一万字,我想,大概没有其他日语文章像这样详细地解释过 SELFIES。我希望通过这份努力,能让更多身边的人开始使用 SELFIES,并促成更多关于其在实际应用中的优缺点(Pros and Cons)的讨论机会。
此外,由于这篇文章是比较即兴地写成的,其中可能存在一些错误。如果您发现了问题,还请不吝指正,非常感谢!
参考资料
@steroidinlondon 的文章:《请问您今天要来点化合物吗?~医药化学录~》(译者注:此处neta自芳文社著名漫画点兔)
官方 GitHub 页面:
一篇详尽的英文博客文章:
官方文档:
一些思考
为了加深自己对SELFIES这种分子表示方法的理解,我尝试着翻译了这篇短小的博客(语法上还是十分生硬,请多包涵)。了解了SELFIES的基本原理之后,我便对这种表示方法所宣传的'100% robust'产生了疑问。
MolGen是一个以SELFIES为输入和输出的、预训练的BART (Bidirectional and Auto-Regressive Transformers) 架构分子生成模型。在使用MolGen生成分子时,经常会出现如下情况:
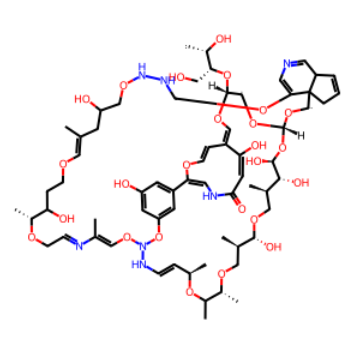
它是基于下面这个分子生成出来的:
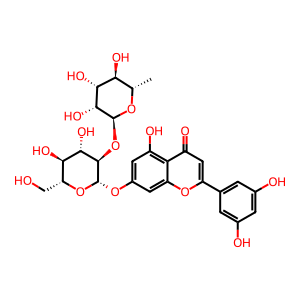
可以注意到,MolGen模型在生成分子时,把分子中本来的六元环或是拆开、或是向环里添加原子,有时还会生成出超大的环结构;并且有的分支结构会连接到显然不可能连接的地方。这类分子对Rdkit来说是合理的,但从化学角度可以说是无意义的。
什么原因导致了这种现象呢?这个问题并不复杂。对MolGen来说,每个被方括号括起来的字符串都算作一个token,在输入和输出时的地位是平等的;但不应如此,因为SELFIES中的索引符号虽然看起来形如[C]、[Branch1]等,但它们只用以计算Q值进而确定环/分支结构连接到哪个原子上。那么模型在自回归的生成过程中,一旦修改了这些索引符号,就会导致基团被连接到错误的地方,进而使分子突变。因此,SELFIES真的是100% robust的吗?从Rdkit读取分子的角度来看是的,但这不一定代表分子有意义。
解决这一问题的核心思想是阻止深度生成模型(或其他种类的模型)对SELFIES中的环符号、分支符号和索引符号进行修改。一个简单的实现方法是使用正则表达式识别其中的环和分支符号,再在其中检索那个“用于表示环/分支符号后有多少个符号是索引符号”的数字,将上述三种符号列为禁止修改的token,这样就可以基本防止分子骨架突变(仍有极个别情况可能导致突变)。
